Programming Parallel Computers
Introduction
All modern computers have at least two processors:
- CPU, the central processing unit, which is what we have been using so far in this course, and
- GPU, the graphics processing unit, which we have left so far unused.
Earlier GPUs had only special primitives related to 3D graphics, but nowadays they are massively-parallel processors that we can use for any kind of computations.
How much performance in theory?
There are lots of different kinds of GPUs available on the market, with vastly different performance profiles. Typically, in a modern computer there is usually more computing power on the GPU than on the CPU, but it might be more challenging to put all of that in practical use.
Let us look at a concrete example, the computers that we have in our classroom:
| CPU | GPU | |
|---|---|---|
| Model: | Intel Xeon E3-1230v5 | NVIDIA Quadro K2200 |
| Architecture: | “Skylake” | “Maxwell” |
| Clock frequency: | 3.4–3.8 GHz | 1.0–1.1 GHz |
| Parallel high-level units: | 4 cores | 5 streaming multiprocessors |
| Parallel single-precision arithmetic units: | 64 | 640 |
| Parallel double-precision arithmetic units: | 32 | 20 |
| Single-precision operations per second: | 460 billion | 1400 billion |
| Double-precision operations per second: | 230 billion | 45 billion |
We are already familiar with the parallelism that we have in the CPU. For example, if we are doing single-precision arithmetic operations:
- we can use 4 cores (multicore parallelism),
- each of them has 2 units for vector operations (superscalar execution),
- each of them can do arithmetic with 8-wide vectors (vectorization), and
- we can achieve a throughput of 1 operation per clock cycle (pipelining).
Hence there are in total 4 × 2 × 8 = 64 parallel arithmetic units. With a clock frequency of 3.6 GHz we can achieve in total 64 × 3.6 ≈ 230 billion operations per second, and if we cheat a bit by using FMA operations and count them as one multiplication and one addition, we get the final number of 460 billion operations per second.
GPUs are very different. As we can see in the table, we have got more parallel units but they work at a lower clock speed. The bottom line is that we could do roughly 3 times more single-precision operations with the GPU than with the CPU — provided that we can indeed split our work among the hundreds of arithmetic units, without hitting other bottlenecks.
It is also good to note that if we need double-precision floating-point operations on these computers, it is probably a good idea to avoid the GPU whenever possible.
How much performance in practice?
In this chapter we will continue with the running example that we solved with the CPU in Chapter 2: the problem of finding cheapest two-hop paths in a directed graph.
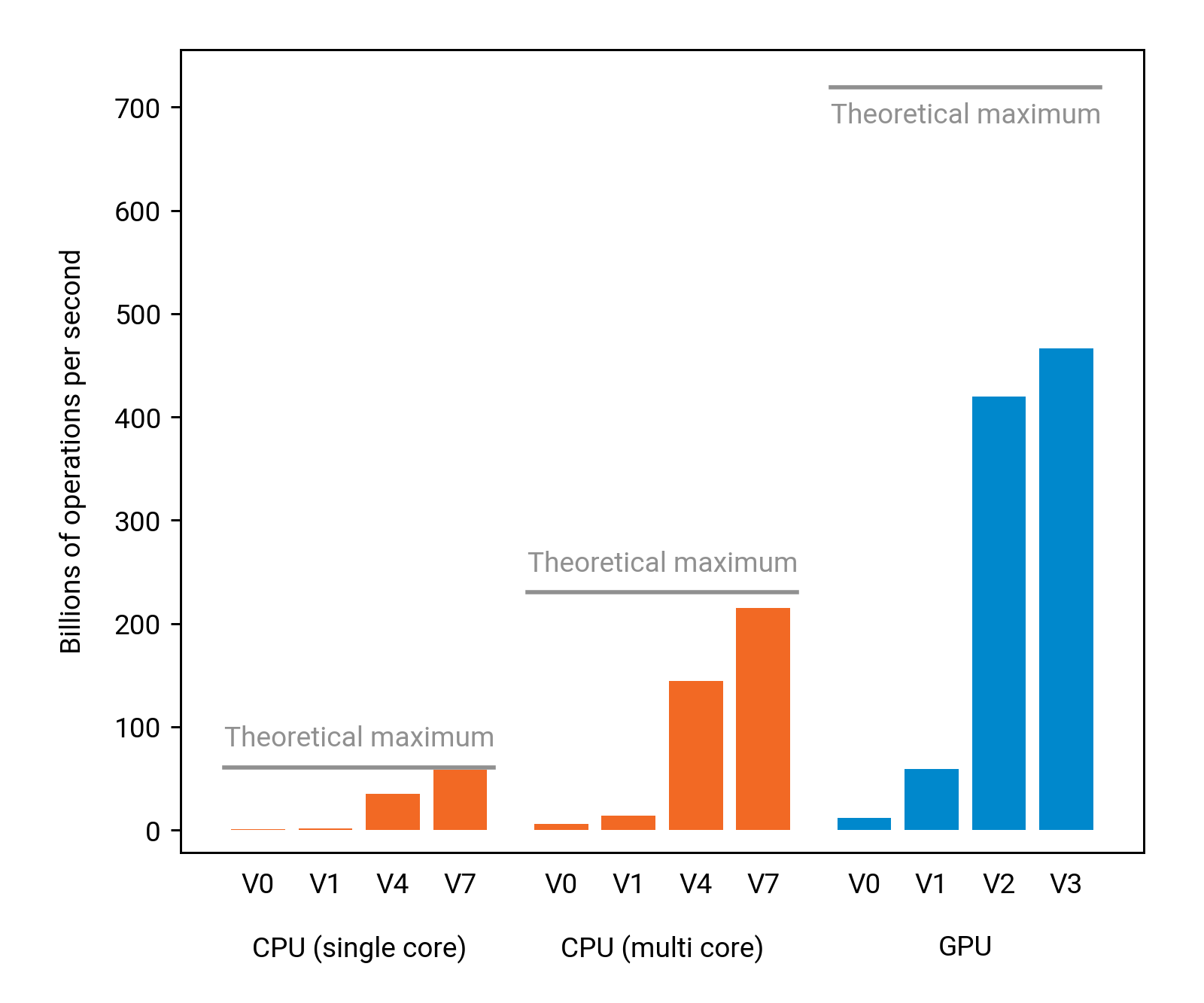
We will again develop a number of solutions, each of them making more use of the parallel computing resources of the GPU. As we already got the running time down to less than 1 second for n = 4000 with CPUs, we will switch to n = 6300 here to get more tangible running times. With such an input size, using the classroom computers, our baseline CPU solution takes 397 seconds and the fastest CPU solution takes 2 seconds. Using GPUs, we can improve the running time to 1.1 seconds in practice — a rather significant improvement:
However, as we see in the above figure, some care is needed — the first GPU solutions that we will develop are no faster than what we could do with a single-core CPU. We will have the same challenges with GPUs as what we had with CPUs: we must have sufficiently many independent operations ready for execution, and we must be careful to heavily reuse whatever data we have fetched from the memory.