Programming Parallel Computers
Why do we need parallelism?
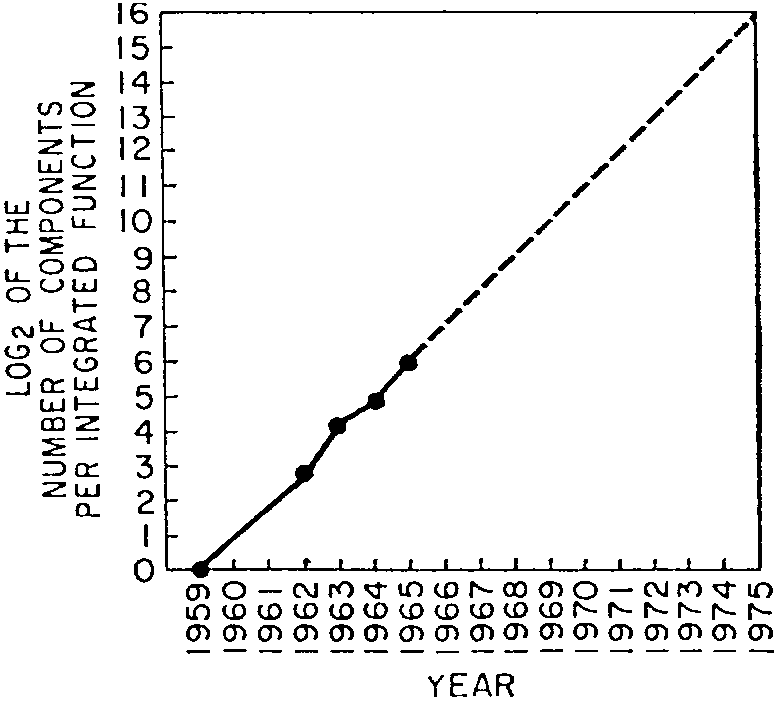
In 1965, Gordon E. Moore had a data set with five data points: how many components there were in state-of-the-art integrated circuits in 1959, 1962, 1963, 1964, and 1965. Here is a visualization of the data from his 1965 paper, “Cramming more components onto integrated circuits”, Electronics Magazine (reprinted in Proc. IEEE, vol. 86, issue 1, 1998):
Based on this data, he made the famous prediction: the number of transistors in an integrated circuit grows exponentially.
While the original rate of the transistor count doubling every year has slowed down somewhat, it is amazing to see that the exponential growth still continues today — we have seen more than 50 years of exponential growth in the packing density of microprocessors:
| Year | Transistors | CPU model |
|---|---|---|
| 1975 | 3 000 | 6502 |
| 1979 | 30 000 | 8088 |
| 1985 | 300 000 | 386 |
| 1989 | 1 000 000 | 486 |
| 1995 | 6 000 000 | Pentium Pro |
| 2000 | 40 000 000 | Pentium 4 |
| 2005 | 100 000 000 | 2-core Pentium D |
| 2008 | 700 000 000 | 8-core Nehalem |
| 2014 | 6 000 000 000 | 18-core Haswell |
| 2017 | 20 000 000 000 | 32-core AMD Epyc |
| 2023 | 90 000 000 000 | M3 Max |
But what about performance?
However, the end user of a computer does not really care that much about the number of transistors; what matters is the performance.
Until around 2000, we used to see the performance of CPUs rapidly increasing, primarily for two reasons. First, the clock speed of the CPU (the number of clock cycles per second) increased:
| Year | Transistors | Clock speed | CPU model |
|---|---|---|---|
| 1975 | 3 000 | 1 000 000 | 6502 |
| 1979 | 30 000 | 5 000 000 | 8088 |
| 1985 | 300 000 | 20 000 000 | 386 |
| 1989 | 1 000 000 | 20 000 000 | 486 |
| 1995 | 6 000 000 | 200 000 000 | Pentium Pro |
| 2000 | 40 000 000 | 2 000 000 000 | Pentium 4 |
Second, CPUs were using fewer and fewer clock cycles per operation. As a simple example, consider the FMUL instruction that multiplies two 80-bit floating point numbers on Intel CPUs. The total latency of the instruction (roughly speaking, the time it takes to launch multiplication to the time when the result is available) has dropped significantly over the years:
| Year | Clock cycles | CPU model |
|---|---|---|
| 1980 | 100 | 8087 |
| 1987 | 50 | 387 |
| 1993 | 3 | Pentium |
The joint effect of increasing clock speeds and decreasing instruction latencies implied massive improvements in the performance. In just a couple of decades, the time it took to complete a floating point multiplication decreased several orders of magnitude, from tens of microseconds to tens of nanoseconds.
After 2000
Around year 2000, everything changed. Moore's law was still doing fine, and the number of transistors kept increasing. However, clock speeds stopped improving. The clock speed of a modern computer is almost always somewhere in the ballpark of 2–4 GHz:
| Year | Transistors | Clock speed | CPU model |
|---|---|---|---|
| 1975 | 3 000 | 1 000 000 | 6502 |
| 1979 | 30 000 | 5 000 000 | 8088 |
| 1985 | 300 000 | 20 000 000 | 386 |
| 1989 | 1 000 000 | 20 000 000 | 486 |
| 1995 | 6 000 000 | 200 000 000 | Pentium Pro |
| 2000 | 40 000 000 | 2 000 000 000 | Pentium 4 |
| 2005 | 100 000 000 | 3 000 000 000 | 2-core Pentium D |
| 2008 | 700 000 000 | 3 000 000 000 | 8-core Nehalem |
| 2014 | 6 000 000 000 | 2 000 000 000 | 18-core Haswell |
| 2017 | 20 000 000 000 | 3 000 000 000 | 32-core AMD Epyc |
| 2023 | 90 000 000 000 | 4 000 000 000 | M3 Max |
Instruction latencies have not improved much, either; sometimes the latencies are nowadays worse than what we saw twenty years ago. Here are examples of the latency of the FMUL operation:
| Year | Clock cycles | CPU model |
|---|---|---|
| 1980 | 100 | 8087 |
| 1987 | 50 | 387 |
| 1993 | 3 | Pentium |
| 2018 | 5 | Coffee Lake |
Since 2000, the number of transistors in a state-of-the-art CPU has increased by more than two orders of magnitude, but this is not visible in the performance if we look at the time it takes to complete a single instruction. A single floating point multiplication took roughly 2 nanoseconds in 2000, and it still takes roughly 2 nanoseconds today.
So what is happening? And why are the CPU manufacturers packing more and more transistors in the CPUs if it does not seem to help with the performance?
New kind of performance
To understand what is happening, we will need to define two terms.
- Latency: time to perform an operation from start to finish.
- Throughput: how many operations are completed per time unit, in the long run.
Example: a massively parallel university
The latency of completing a Master's degree at Aalto University is roughly 2 years. However, the throughput of Aalto is nowadays 1960 degrees/year.
If Aalto educated students in a strictly sequential manner, keeping only 1 student at a time in the “pipeline”, we would have a throughput of only approx. 0.5 degrees/year.
However, Aalto is massively parallel; we have thousands of students in the pipeline simultaneously, and this makes it possible to obtain a throughput that is much higher than 1/latency.
Modern CPUs do exactly the same thing as our university: they are able to keep several instructions in execution simultaneously, and hence they can obtain a much higher throughput than what one would expect based on the instruction latency.
It is hard to design CPUs that have multiplication units with a very small latency. However, throughput is — at least in principle — relatively easy to improve: just add more parallel multiplication units that can be used simultaneously. Another technique that is heavily used in modern processors is pipelining: Arithmetic units can be seen as a long pipeline. At each clock cycle, we can push one new operation into the pipeline. It takes a while for each individual operation to finish, but in the steady state if we initiate one operation per clock cycle, we will also finish one operation per clock cycle:
| Time | Start | In progress | Finish |
|---|---|---|---|
| 0 | operation A | ||
| 1 | operation B | A | |
| 2 | operation C | B, A | |
| 3 | operation D | C, B, A | |
| 4 | operation E | D, C, B, A | |
| 5 | operation F | E, D, C, B | A |
| 6 | operation G | F, E, D, C | B |
| 7 | operation H | G, F, E, D | C |
| 8 | operation I | H, G, F, E | D |
| 9 | operation J | I, H, G, F | E |
| 10 | operation K | J, I, H, G | F |
| 11 | operation L | K, J, I, H | G |
Thanks to pipelining, each arithmetic unit typically has a throughput of 1 operation per clock cycle, and modern CPUs have a large number of parallel arithmetic units. For example, in a typical modern CPU there are 16 parallel units for single-precision floating point multiplications per core. Hence, a modern 4-core CPU can do floating point multiplications at a throughput of 64 operations per clock cycle, or roughly 200 billion operations per second (recall that the clock speed is typically around 3 GHz, i.e., 3 billion clock cycles per second).
This is a dramatic improvement in comparison with the CPUs from the 1990s, in which the throughput of floating point multiplications was typically in the ballpark of 0.5 operations per clock cycle.
In summary, the performance of modern CPUs is steadily increasing, but it is new kind of performance: the latency of individual operations is not improving at all, only throughput is improving. And to benefit from the new kind of performance, we will need new kind of software that explicitly takes into account the difference between throughput and latency.
With old code, a computer from 2025 is not any faster than a computer from 2000. In this course we will learn how to write new code that is designed with modern computers in mind.