In this chapter we will look at a simple graph problem and see how to solve it so that we are using close to 100% of the theoretical maximum performance of the computer.

The shortcut problem

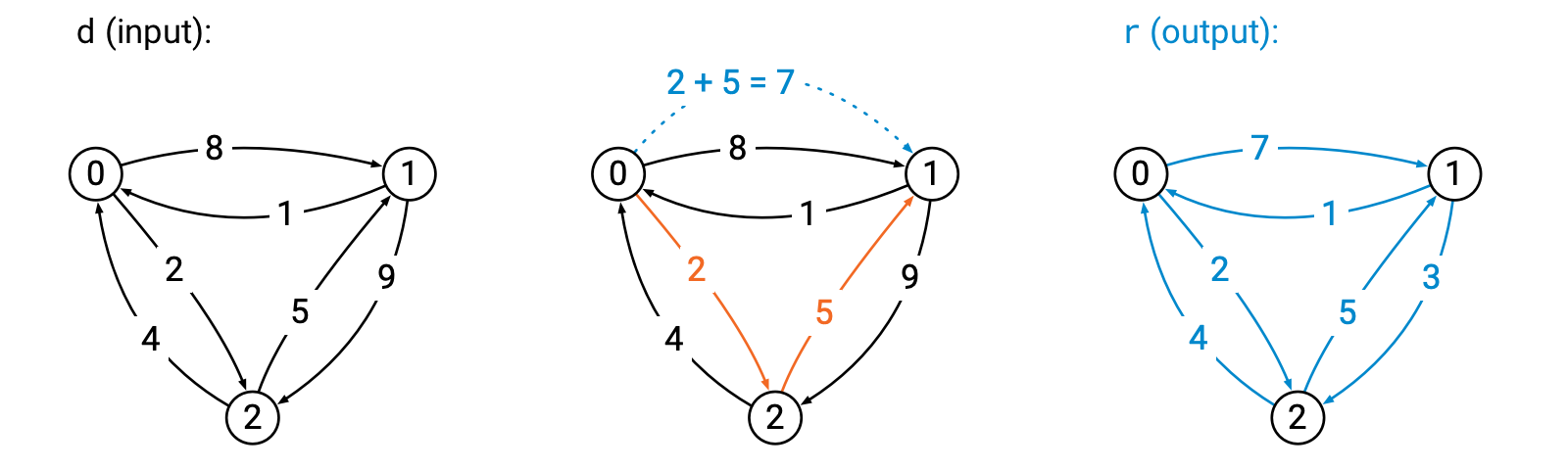
We will use the following simple graph problem as our running example throughout this chapter. We have a directed graph with $n$ nodes. The nodes of the graph are labeled with numbers $0,1,\dotsc,n-1$. There is a directed edge between each pair of the nodes; the cost of the edge between nodes $i$ and $j$ is $d_{ij}$; we will assume that $d_{ij}$ is a nonnegative real number. For convenience, we write $d_{ii} = 0$ for each node $i$.

However, the costs do not necessarily satisfy the triangle inequality. We might have an edge of cost $d_{ij} = 10$ from node $i$ to $j$, but there might be an intermediate node $k$ with $d_{ik} = 2$ and $d_{kj} = 3$. Then we can follow the route $i \to k \to j$ at a total cost of $2+3 = 5$, while the direct route $i \to j$ would cost $10$.

Our task is to find for all $i$ and $j$ what is the cost of getting from $i$ to $j$ by taking at most two edges. If we write $r_{ij}$ for the result, then clearly $$ r_{ij} = \min_k (d_{ik} + d_{kj}), $$ where $k$ ranges over $0,1,\dotsc,n-1$. Note that we will also consider here e.g. the route $i \to i \to j$, and hence we will also find a path of one edge if it happens to be cheapest.

Remarks [advanced]

We can write the distances $d_{ij}$ as a matrix $D$, and the results $r_{ij}$ as a matrix $R$. Then $R = D \circ D$, where $\circ$ denotes min-plus matrix multiplication.

If we iterate the process and calculate $$ D_2 = D \circ D, \quad D_4 = D_2 \circ D_2, \quad D_8 = D_4 \circ D_4, \quad \dotsc $$ we can quickly find the cost of getting from any node to any other node by following at most $2, 4, 8, \dotsc$ edges. Iterating this operation for a logarithmic number of times would therefore also give all-pairs shortest path distances (but recall that there are more direct ways of solving the all-pairs shortest path problem).

Interface

We will implement a C++ function step with the following prototype:

void step(float* r, const float* d, int n);

Here n denotes the number of nodes, d contains the input, and r will contain the result. Both d and r are pointers to arrays with n * n floats.

The cost of the edge from node i to node j is stored in d[n*i + j]. Similarly, the cost of getting from i to j by following at most two edges will be stored in r[n*i + j]. Here 0 <= i < n and 0 <= j < n.

Example

Here is a simple example of how we could call step:

int main() {
    constexpr int n = 3;
    const float d[n*n] = {
        0, 8, 2,
        1, 0, 9,
        4, 5, 0,
    };
    float r[n*n];
    step(r, d, n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            std::cout << r[i*n + j] << " ";
        }
        std::cout << "\n";
    }
}

This program should produce the following output:

0 7 2
1 0 3
4 5 0

Here, for example, there is a direct edge from node 0 to node 1 with cost 8. However, we can take an edge from node 0 to node 2 (cost 2), and then an edge from node 2 to node 1 (cost 5), which results in a path of total cost 7.