In the previous version, we read 6 vectors from memory to registers, and then we are able to do 9 + 9 useful vector operations with this data. On average, the ratio of arithmetic operations to memory accesses is 3 to 1.

We will now develop a solution in which we only read 2 vectors from memory to registers, and then we will do 8 + 8 useful vector operations with this data. We can improve the ratio to 8 to 1.

Basic idea

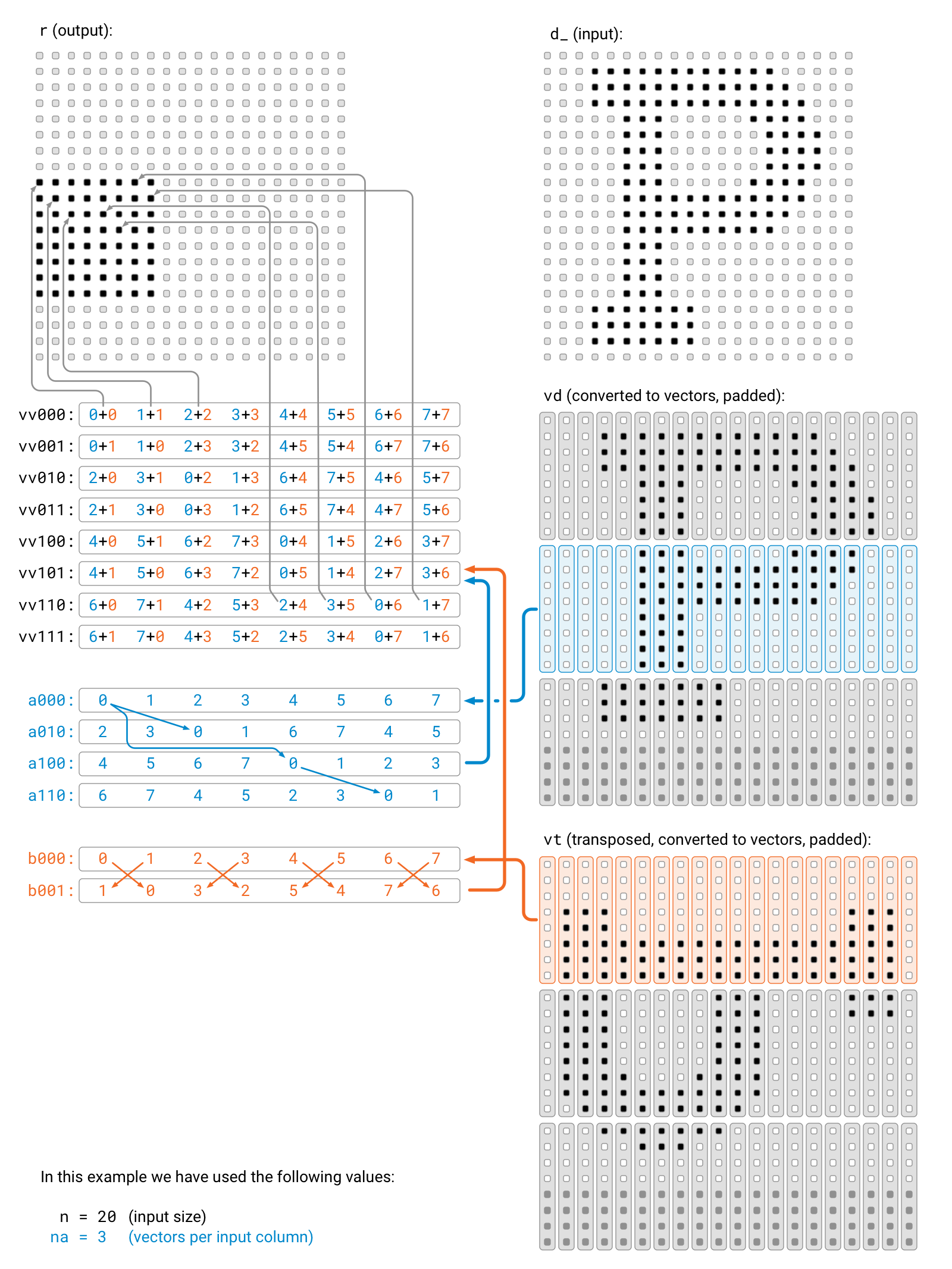
In V3 and V4, one vector represented 8 elements from the same row. We will now pack data in vectors in a different manner: one vector will represent 8 elements from the same column. The high-level idea is illustrated in the following picture.

In essence, we will try to compute an entire 8 × 8 block of the result in one pass. Let us first see what are the main challenges. Using the memory layout sketched in the above figure, let a be the first vector of the blue area of vd and let b be the first vector of the orange area of vt. Now a and b hold enough information that would be sufficient to update all 8 × 8 values in the black part of the result array r.

However, the key challenge is that we would like to calculate all 8 × 8 pairwise sums between the elements of a and b efficiently with the help of vector operations. The vector addition a + b will only give us these sums:

a[0] + b[0]
a[1] + b[1]
a[2] + b[2]
a[3] + b[3]
a[4] + b[4]
a[5] + b[5]
a[6] + b[6]
a[7] + b[7]

How do we get everything else, including e.g. a[4] + b[7] and a[5] + b[2]?

The first idea might be to rotate one of the vectors, so that we find e.g. a vector b1 with

b1[0] = b[1]
b1[1] = b[2]
b1[2] = b[3]
b1[3] = b[4]
b1[4] = b[5]
b1[5] = b[6]
b1[6] = b[7]
b1[7] = b[0]

Now we could calculate a + b1, rotate b1 again to obtain b2, calculate a + b2, etc. This way we would find all pairwise sums, and we could update all pairwise minimums. Unfortunately, rotating an entire AVX vector on Intel CPUs is a rather expensive operation, and we would need to do 7 such rotations in total.

Choosing the right permutations

We can do better by applying the scheme that we show in the above figure. We start with the original vectors a000 and b000. Then we permute the elements as follows:

a100 = swap4(a000);
a010 = swap2(a000);
a110 = swap2(a100);
b001 = swap1(b000);

The “swap” operations reorder vectors as follows:

The swap operations are not something that we will have readily available. However, Intel CPUs have instructions vperm2f128 and vpermilps that we can use to implement these operations efficiently, and we can access these operations from a C++ program with the help of the intrinsic functions _mm256_permute2f128_ps and _mm256_permute_ps — these are available from #include <x86intrin.h>.

It takes a while to figure out the right parameters, but you can verify that the following functions indeed do the trick:

static inline float8_t swap4(float8_t x) { return _mm256_permute2f128_ps(x, x, 0b00000001); }
static inline float8_t swap2(float8_t x) { return _mm256_permute_ps(x, 0b01001110); }
static inline float8_t swap1(float8_t x) { return _mm256_permute_ps(x, 0b10110001); }

Now we only need to do 4 permutations, we will have 4 + 2 vectors, and if we calculate all 4 × 2 pairwise sums of these vectors, we will be able to construct all 8 × 8 pairwise sums of the vector elements.

For example, can we find a000[4] + b000[7] somewhere? Yes, sure: a010[6] = a000[4] and b001[6] = b000[7], so a010 + b001 will contain a000[4] + b000[7] in element 6.

The main drawback here is that the elements of the result are stored in a somewhat awkward order. As we can see in the figure, some additional effort is needed to move the right element of the vectors to the right location of the result array.

Implementation

Here is our implementation of the above idea. The innermost loop is straightforward, but some thinking is needed to check that the part that copies data from vv... variables to the result array actually does the right job.

void step(float* r, const float* d_, int n) {
    // vectors per input column
    int na = (n + 8 - 1) / 8;

    // input data, padded, converted to vectors
    std::vector<float8_t> vd(na * n);
    // input data, transposed, padded, converted to vectors
    std::vector<float8_t> vt(na * n);

    #pragma omp parallel for
    for (int ja = 0; ja < na; ++ja) {
        for (int i = 0; i < n; ++i) {
            for (int jb = 0; jb < 8; ++jb) {
                int j = ja * 8 + jb;
                vd[n*ja + i][jb] = j < n ? d_[n*j + i] : infty;
                vt[n*ja + i][jb] = j < n ? d_[n*i + j] : infty;
            }
        }
    }

    #pragma omp parallel for
    for (int ia = 0; ia < na; ++ia) {
        for (int ja = 0; ja < na; ++ja) {
            float8_t vv000 = f8infty;
            float8_t vv001 = f8infty;
            float8_t vv010 = f8infty;
            float8_t vv011 = f8infty;
            float8_t vv100 = f8infty;
            float8_t vv101 = f8infty;
            float8_t vv110 = f8infty;
            float8_t vv111 = f8infty;
            for (int k = 0; k < n; ++k) {
                float8_t a000 = vd[n*ia + k];
                float8_t b000 = vt[n*ja + k];
                float8_t a100 = swap4(a000);
                float8_t a010 = swap2(a000);
                float8_t a110 = swap2(a100);
                float8_t b001 = swap1(b000);
                vv000 = min8(vv000, a000 + b000);
                vv001 = min8(vv001, a000 + b001);
                vv010 = min8(vv010, a010 + b000);
                vv011 = min8(vv011, a010 + b001);
                vv100 = min8(vv100, a100 + b000);
                vv101 = min8(vv101, a100 + b001);
                vv110 = min8(vv110, a110 + b000);
                vv111 = min8(vv111, a110 + b001);
            }
            float8_t vv[8] = { vv000, vv001, vv010, vv011, vv100, vv101, vv110, vv111 };
            for (int kb = 1; kb < 8; kb += 2) {
                vv[kb] = swap1(vv[kb]);
            }
            for (int jb = 0; jb < 8; ++jb) {
                for (int ib = 0; ib < 8; ++ib) {
                    int i = ib + ia*8;
                    int j = jb + ja*8;
                    if (j < n && i < n) {
                        r[n*i + j] = vv[ib^jb][jb];
                    }
                }
            }
        }
    }
}

Results

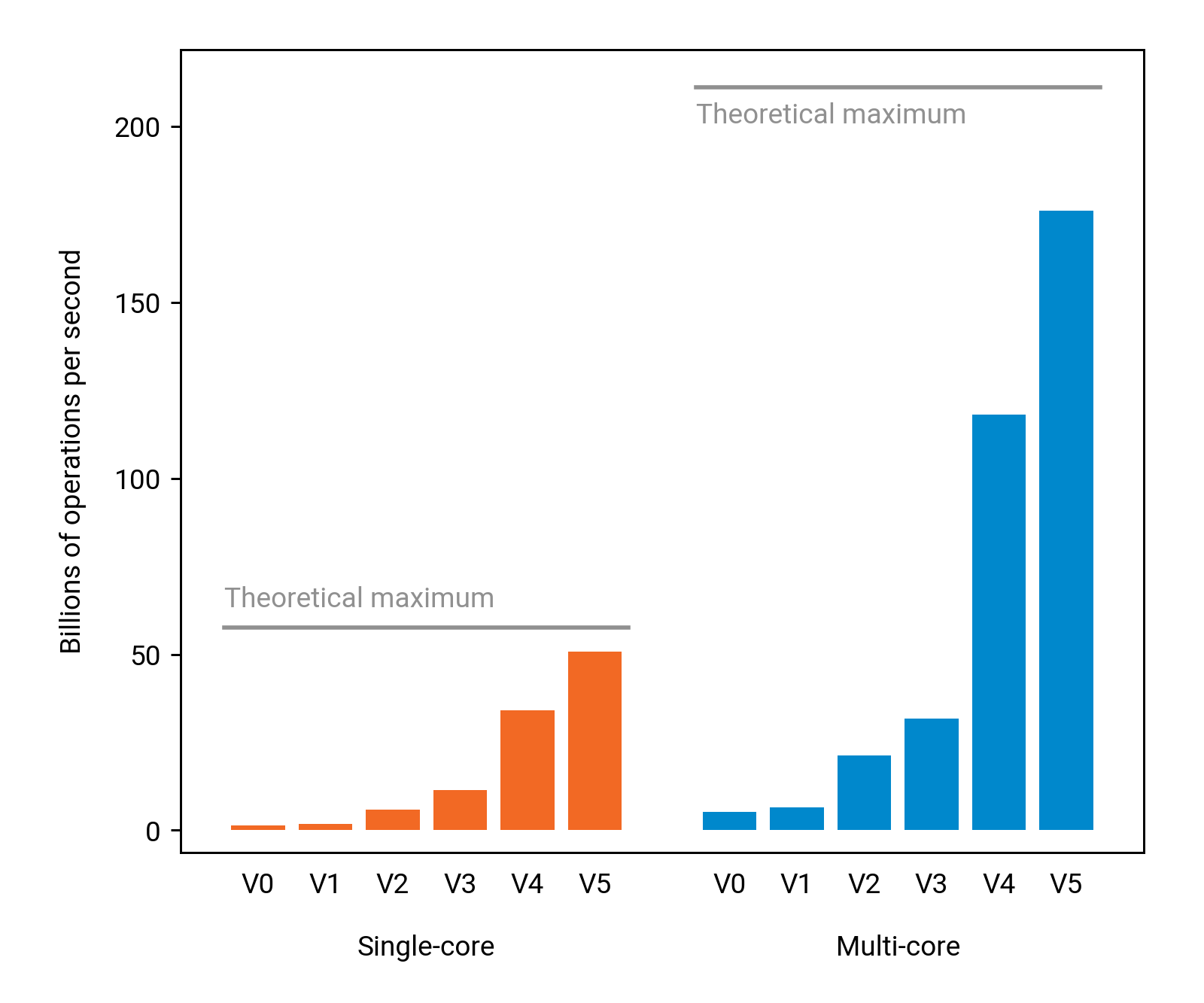
We are now rapidly approaching the theoretical limitations of the CPU:

The running time for n = 4000 is now only 0.7 seconds. We have improved the running time over the baseline by a factor of 136.