When we do not have any bottlenecks, a modern CPU is typically able to execute 3–4 machine language instructions per clock cycle per core. Nevertheless, the CPU that we use in our examples is able to perform up to 32 floating point operations per clock cycle per core. To achieve this, we will clearly need to do a lot of work with one instruction.

Vector registers

In our CPU we have got 256-bit wide vector registers and special machine-language instructions that do operations with such registers.

Each single-precision floating point number takes 32 bits, so we can pack 8 floats in one 256-bit register. That is, one register can store as much data as the following array:

float x[8];

Vector instructions can manipulate such 8-element vectors very efficiently. For example, we can perform elementwise addition of 8-element vectors with one instruction:

vaddps %ymm0, %ymm1, %ymm2

This is, in essence, equivalent to the following C++ code; here I use x for the 8-element vector that is kept in register %ymm0, and similarly y and z for %ymm1 and %ymm2:

z[0] = x[0] + y[0];
z[1] = x[1] + y[1];
z[2] = x[2] + y[2];
z[3] = x[3] + y[3];
z[4] = x[4] + y[4];
z[5] = x[5] + y[5];
z[6] = x[6] + y[6];
z[7] = x[7] + y[7];

There are two execution ports that can execute vaddps instructions, each at a throughput of 1 instruction per clock cycle. Hence, each CPU core can complete 16 single-precision floating point additions per clock cycle.

There are also similar instructions for doing elementwise comparison and for calculating elementwise minimum, maximum, subtraction, multiplication, and division. Hence, there is a lot of computing power available, but this does not come for free:

1. We have to reorganize our algorithm so that we can exploit elementwise operations. This naturally requires that there are lots of similar, independent operations that we need to run at each step.
2. We have to instruct the compiler to generate code that makes use of the vector registers and vector instructions.

Sometimes we may be lucky and a modern compiler might automatically “vectorize” our program for us. But as we have seen, this is not the case here; we have studied the assembly code of all prior versions, and we have not encountered any vector instructions such as vaddps.

Some terminology

People often refer to “vector instructions”, “SIMD instructions”, and “AVX instructions” more or less interchangeably:

• SIMD (single instruction, multiple data) is a general term for this kind of parallelism: we apply a single operation (e.g. addition) to multiple data elements (e.g. 8 floating point numbers packed in a single vector register).
• AVX (Advanced Vector Extensions) is the name for the specific set of vector registers and vector instructions that we have in recent Intel CPUs.

In practice, AVX instructions are available in most of the computers that we use nowadays; it has been available in Intel and AMD processors since 2011. In AVX, there are 16 vector registers that are 256-bit wide, and there are instructions that can use such registers e.g. as a vector of 8 floats or as a vector of 4 doubles.

Vector types in C++ code

There are many different ways of using vector operations in C++ code. Many programmers use so-called intrinsic instructions that provide very low-level access to the vector operations. However, there is also a much more programmer-friendly approach: many modern C++ compilers support convenient “vector types”.

For example, in GCC and Clang we can define a type called float8_t (you are free to pick any other name) that is a vector of 8 floats, as follows:

typedef float float8_t __attribute__ ((vector_size (8 * sizeof(float))));

The definition looks a bit ugly, but it is something we only need to use once, and we can simply copy-paste it to each program in which we want to use vector types.

Now we can introduce variables of type float8_t, and it will behave very much like an array of 8 floats. However, we can apply the usual arithmetic operators such as + and * to the entire vector. Here is a simple example:

float8_t a, b, c;

a = ...;
b = ...;
c = a + b;

The behavior of this code is very similar to the following:

float a[8], b[8], c[8];

a = ...;
b = ...;
c[0] = a[0] + b[0];
c[1] = a[1] + b[1];
c[2] = a[2] + b[2];
c[3] = a[3] + b[3];
c[4] = a[4] + b[4];
c[5] = a[5] + b[5];
c[6] = a[6] + b[6];
c[7] = a[7] + b[7];

However, the performance differs a lot. In the first version, the compiler will try to keep a, b, and c in vector registers, and the single operation c = a + b will get translated into one vector instruction (vaddps), instead of doing 8 scalar operations (vaddss).

We can refer to individual elements of vector types. For example, if we have float8_t a, it is possible to write e.g. a[0] = 3 * a[1] + 2, and it will do exactly what we would expect it to do. However, such operations tend to be slow — the compiler has to generate code that extracts one element of the vector and updates another. In particular, this does not take any advantage of the performance of vector instructions.

Hence our goal is to redesign the program so that we can use vector-wide operations such as a + b, where both a and b are of type float8_t. Only then we will get efficient code.

Warning: proper memory alignment needed

Most of the time, we can use vector types just like any other type in a C++ program. We can pass vectors as a parameter to a function, we can return vectors, we can use vectors as local variables, and we can even introduce arrays of vectors as local variables. The compiler will do the right job, just like for variables of any other type. Variables will be kept in vector registers whenever possible, and otherwise the compiler will use the stack as needed. For example, the following code works just fine:

float8_t example(float8_t a, float8_t b) {
    float8_t c[2];
    c[0] = a + b;
    c[1] = a - b;
    float8_t d = c[0] * c[1];
    return d;
}

However, whenever we do dynamic memory allocation, we will have to be careful with memory alignment.

If you use a pointer to vector data (e.g. float8_t* p), you must make sure that it points to a block of memory that is properly aligned. The memory address has to be a multiple of 32. In essence, vector types are a contract between the programmer and the compiler:

• If you use vector pointers, you promise that it always points to a piece of memory that is properly aligned.
• The compiler can then make use of this promise when it generates code. It might, for example, generate memory access instructions that only work with properly aligned memory.

If you break the rules, it is highly likely that your program will crash.

For example, the following function is seriously broken:

void crash() {
    float8_t a = {1,2,3,4,5,6,7,8};
    float8_t* p = (float8_t*)malloc(sizeof(float8_t));
    float8_t* q = (float8_t*)malloc(sizeof(float8_t));
    std::cout << p << "\n";
    std::cout << q << "\n";
    *p = a;
    *q = a;
    a = *p + *q;
    std::cout << a[0] << "\n";
    free(p);
    free(q);
}

Here is what might happen when we run it on Linux:

0x117d030
0x117d060
segmentation fault

Here we were accidentally lucky with the allocation of q and the memory address happened to be a multiple of 32 (0x20), but we were unlucky with the allocation of p. When we reach the line *p = a, the program crashes. Here is what we see if we run it under GDB debugger:

Program received signal SIGSEGV, Segmentation fault.
crash () at crash.cc:99
99          *p = a;

If we check the assembly code in the debugger, we see that the offending instruction was vmovaps %ymm0,(%r12), and indeed, the documentation of the instruction vmovaps says that it can only be used to transfer data between registers and properly aligned memory addresses. The compiler was free to use such an instruction, as we had declared p to be a pointer to float8_t, which implies that we will take care of proper memory alignment.

There are many ways to guarantee aligned memory allocation. Starting with C++17, you can simply use the standard containers together with vector types, like this:

// We assume that you use a modern C++ compiler and compile with -std=c++17
std::vector<float8_t> x(10);

Here we allocated properly aligned memory for an array of 10 vectors, and we can safely refer to x[0], x[1], …, x[9].

On older compilers, you could use, e.g., the posix_memalign function; this is available on both Linux and macOS. There is also aligned_alloc in the C11 and C++17 standard libraries, which can be a more portable alternative. Note that if you use these functions, you also assume responsibility of correctly freeing the memory once it is no longer needed. This makes their use more error-prone, and we recommend, especially in the context of this course, to use std::vector when possible.

Implementation

Let us start with some basic definitions and helper functions.

constexpr float infty = std::numeric_limits<float>::infinity();

constexpr float8_t f8infty {
    infty, infty, infty, infty,
    infty, infty, infty, infty
};

static inline float hmin8(float8_t vv) {
    float v = infty;
    for (int i = 0; i < 8; ++i) {
        v = std::min(vv[i], v);
    }
    return v;
}

static inline float8_t min8(float8_t x, float8_t y) {
    return x < y ? x : y;
}

Here hmin8 calculates a “horizontal minimum” of one vector, while min8 calculates the elementwise minimum of two vectors. For example, assume that we have:

float8_t a = {1,2,3,4,5,6,7,28};
float8_t b = {11,12,13,14,15,16,17,8};

Then:

hmin8(a) = 1
hmin8(b) = 8
min8(a,b) = {1,2,3,4,5,6,7,8}

As we can see, comparison and the ternary operator ?: work fine with vector types on GCC.

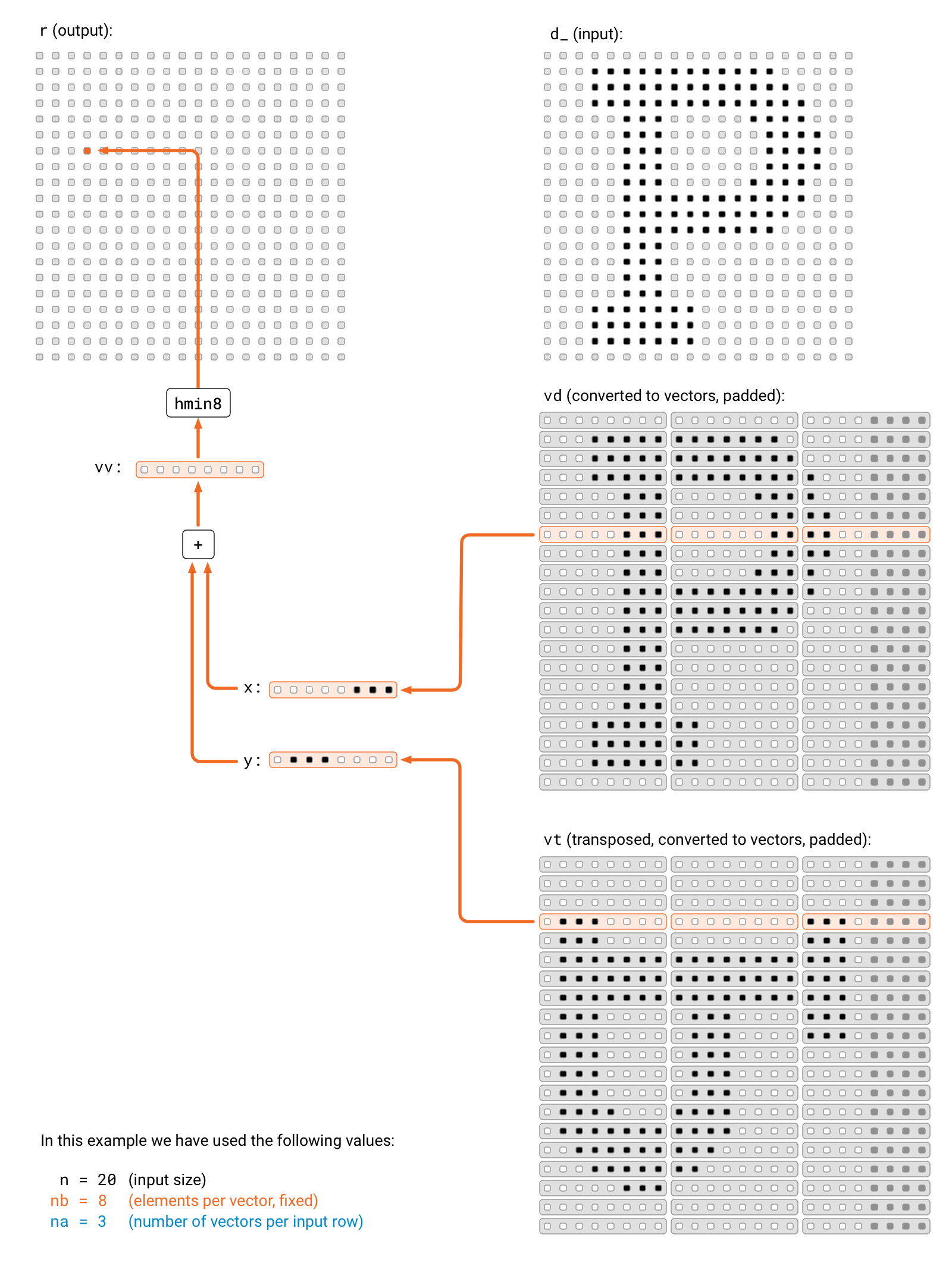
Now we are ready to give the full implementation. The basic idea is very similar to version 2, in which we calculated 4 minimums simultaneously in parallel. Now we calculate 8 minimums simultaneously in parallel, but the key difference is that we can exploit vector operations.

void step(float* r, const float* d_, int n) {
    // elements per vector
    constexpr int nb = 8;
    // vectors per input row
    int na = (n + nb - 1) / nb;

    // input data, padded, converted to vectors
    std::vector<float8_t> vd(n * na);
    // input data, transposed, padded, converted to vectors
    std::vector<float8_t> vt(n * na);

    #pragma omp parallel for
    for (int j = 0; j < n; ++j) {
        for (int ka = 0; ka < na; ++ka) {
            for (int kb = 0; kb < nb; ++kb) {
                int i = ka * nb + kb;
                vd[na*j + ka][kb] = i < n ? d_[n*j + i] : infty;
                vt[na*j + ka][kb] = i < n ? d_[n*i + j] : infty;
            }
        }
    }

    #pragma omp parallel for
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            float8_t vv = f8infty;
            for (int ka = 0; ka < na; ++ka) {
                float8_t x = vd[na*i + ka];
                float8_t y = vt[na*j + ka];
                float8_t z = x + y;
                vv = min8(vv, z);
            }
            r[n*i + j] = hmin8(vv);
        }
    }
}

Note that in the following part, we read two 8-element vectors, we calculate 8 sums in parallel, and then calculate 8 minimums in parallel. In total, we do 16 useful arithmetic operations here. There is a lot of parallel computing happening in this seemingly innocent code fragment:

float8_t x = vd[na*i + ka];
float8_t y = vt[na*j + ka];
float8_t z = x + y;
vv = min8(vv, z);

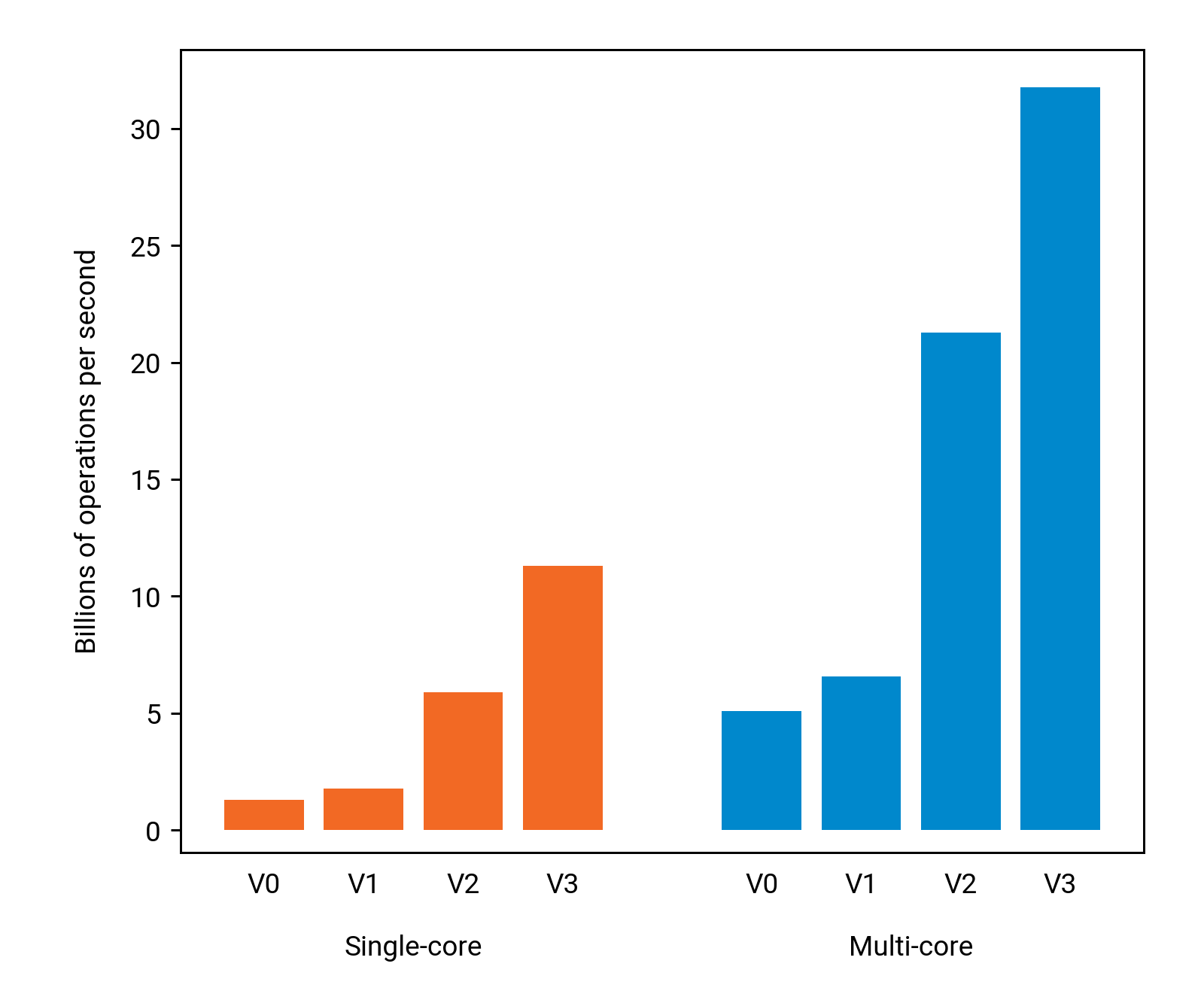
Results

In this application, vector instructions help a lot:

Single-threaded performance improved by a factor of 6.3 in comparison with version 1, and multi-threaded performance improved by a factor of 4.8. The overall running is now only 4 seconds for the version that uses both multi-threading and vector instructions.

Vectorization helped even more than instruction-level parallelism, which is what we tried in version 2. However, this is just a starting point: nothing prevents us from using vector instructions, instruction-level parallelism, and OpenMP simultaneously in the same application. This is exactly what we will attempt to do in the next version.

Vectors of doubles

Instead of using vector registers to store 8 floats, we can equally well use them to store 4 doubles. The correct definition for such a type is:

typedef double double4_t __attribute__ ((vector_size (4 * sizeof(double))));

Then we can use double4_t just like we used float8_t previously. The CPU has similar instructions for doing elementwise manipulations with vectors of 4 doubles, and the performance is similar — the only difference being that we are only performing 4 arithmetic operations per instruction, instead of 8.

Indeed, the main difference between the performance of floats and doubles on modern CPUs is this: with floats, you can pack twice as many operands in vector registers, and hence do twice as much useful work per instruction.