In V2 we achieved a factor-3.3 speedup in comparison with V1 by exploiting instruction-level parallelism, and in V3 we achieved a factor-6.3 speedup in comparison with V1 by exploiting vector instructions. However, if we try to combine both of the techniques, we will not see much improvement in the performance.

The bottleneck will be in the memory system. CPU is much faster in doing arithmetic operations than in getting data from the main memory to the CPU. As a simple example, consider an application that tries to do just lots of single-precision floating-point additions. If all operands are readily available in the CPU registers, each CPU core is able to do 2 vector additions per clock cycle, and each vector contains 8 elements; overall, the entire 4-core CPU could do 64 floating-point additions per clock cycle.

But what would happen if we tried to get all operands from the main memory, without any data reuse in CPU registers or caches? Each floating-point addition needs two operands, a total of 8 bytes. The maximum main memory bandwidth of the CPU that we use is 34.1 GB/s, or approximately 10 bytes per clock cycle. This is enough input data for only 1.25 floating-point additions per clock cycle.

Hence there is a factor-50 difference between how fast we can get operands from the main memory, and how fast the CPU could “consume” operands if they were in the CPU registers. For a maximum performance, we can only afford to fetch 2% of the operands from the main memory; everything else has to come from the cache memory or CPU registers!

Caches are not fast enough to keep the processor busy, either — not even the L1 cache, which is the fastest and smallest cache closest to the processor. Under ideal conditions, each CPU core could read two vectors from the L1 cache per clock cycle, and hence enough operands for, e.g., 1 vector addition per clock cycle per core. However, if all data came from the registers, we could do 2 vector additions per clock cycle per core.

To achieve a good performance, it is necessary to design programs so that we reuse data that we have fetched from the main memory to CPU registers as much as possible.

Opportunities for data reuse

So far all of our implementations have been based on the same basic idea: We calculate each element of the result $r_{ij}$ separately. For example, to find the value of $r_{00}$, we scan row $0$ and column $0$ of the input matrix and calculate the minimum of all pairwise sums $d_{0k} + d_{k0}$. While we do this calculation, there is zero short-term data reuse. Elements $d_{0k}$ and $d_{k0}$ are used only once, and they take part in only one addition. We go through all the trouble of getting $d_{0k}$ and $d_{k0}$ to the CPU, and then immediately throw them away.

However, we could do much better if we reorganize the way we do calculations. We could calculate e.g. $r_{00}$, $r_{01}$, $r_{10}$, and $r_{11}$ in one go. All data that we need to calculate these results is contained in rows $0$ and $1$ and columns $0$ and $1$. We could proceed as follows:

• Read $d_{0k}$, $d_{1k}$, $d_{k0}$, and $d_{k1}$.
• Calculate $d_{0k} + d_{k0}$, $d_{0k} + d_{k1}$, $d_{1k} + d_{k0}$, and $d_{1k} + d_{k1}$.
• Update $r_{00}$, $r_{01}$, $r_{10}$, and $r_{11}$.

Let us now compare this with the naive solution:

• Original: we read 1 row and 1 column to calculate 1 result.
• Improved: we read 2 rows and 2 columns to calculate 4 results.

There is more data reuse by a factor of 2. Each element that we read takes part in 2 additions. The overall number of memory accesses is halved.

This approach gives also another benefit: we have got now independent operations that can be executed in parallel. For example, we can update $r_{00}$, $r_{01}$, $r_{10}$, and $r_{11}$ simultaneously in parallel.

There is also no need to stop here; we can push this idea further. Instead of calculating a 2 × 2 block of the output matrix by scanning 2 rows and 2 columns, we could calculate a 3 × 3 block of the output matrix by scanning 3 rows and 3 columns. We get now more data reuse by a factor of 3, and even more independent operations that give plenty of opportunities for instruction-level parallelism.

Let us implement this idea next.

Implementation

We still use vector operations to do the calculations, exactly the same way as we did in version 3. Each row or column is packed in 8-element vectors, and there is some padding in the last vector if n is not a multiple of 8.

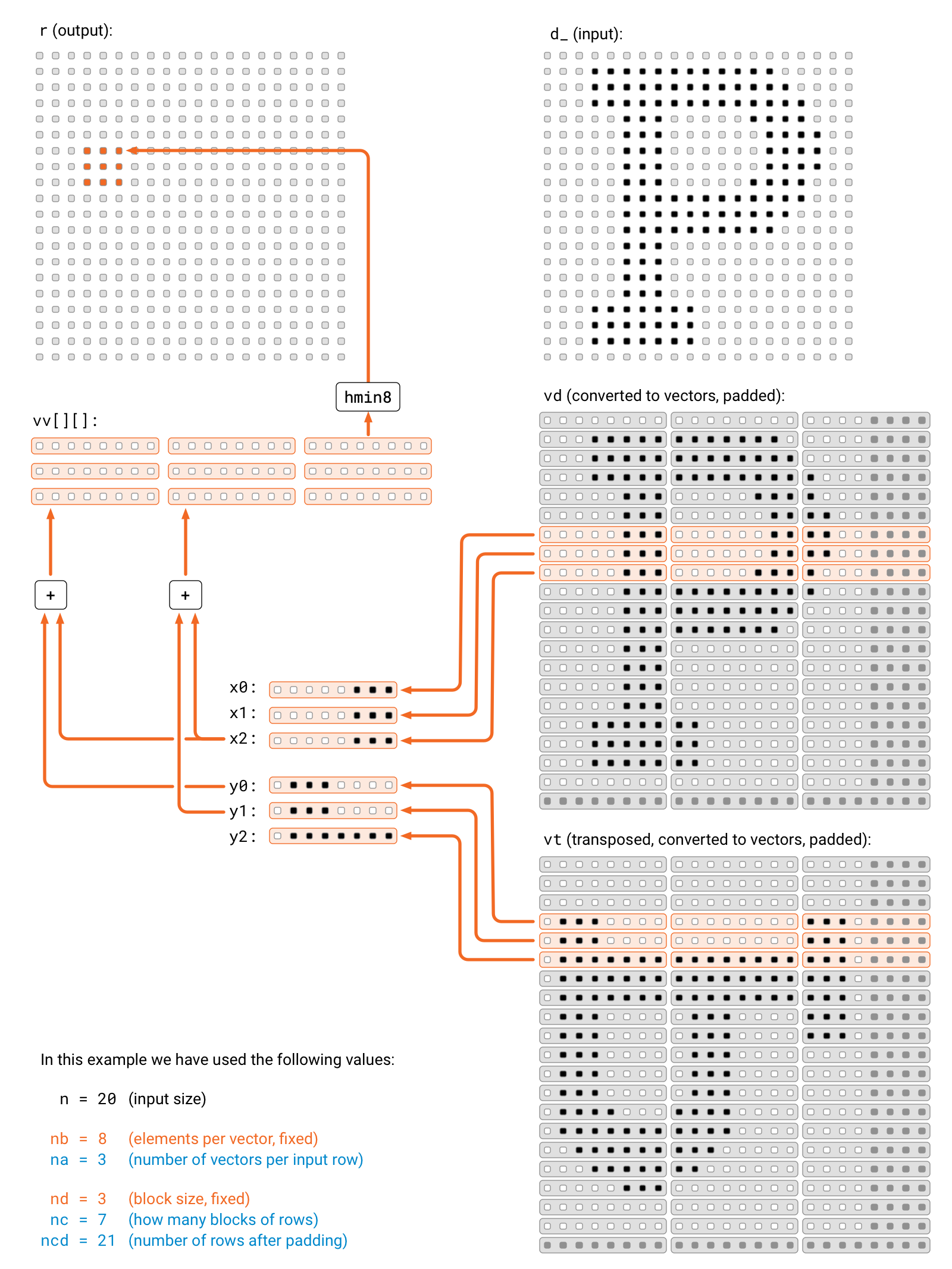
However, the new ingredient is that the innermost loop will not calculate just 1 result, but it will calculate a 3 × 3 block of the result array. We use 9 local variables (array vv) to hold the intermediate results. We use 3 + 3 local variables (x0, x1, x2, y0, y1, and y2) to keep the values that we have read from the memory, and then we will calculate all 3 × 3 pairwise products, reusing data as much as possible.

Again, this is straightforward if n happens to be a multiple of 3. To make our life easy, we will again add some padding. Now e.g. vd is an array whose width is a multiple of 8 (so each row consists of complete 8-element vectors), and its height is a multiple of 3 (so that we can easily process 3 consecutive rows at a time).

void step(float* r, const float* d_, int n) {
    // elements per vector
    constexpr int nb = 8;
    // vectors per input row
    int na = (n + nb - 1) / nb;

    // block size
    constexpr int nd = 3;
    // how many blocks of rows
    int nc = (n + nd - 1) / nd;
    // number of rows after padding
    int ncd = nc * nd;

    // input data, padded, converted to vectors
    std::vector<float8_t> vd(ncd * na);
    // input data, transposed, padded, converted to vectors
    std::vector<float8_t> vt(ncd * na);

    #pragma omp parallel for
    for (int j = 0; j < n; ++j) {
        for (int ka = 0; ka < na; ++ka) {
            for (int kb = 0; kb < nb; ++kb) {
                int i = ka * nb + kb;
                vd[na*j + ka][kb] = i < n ? d_[n*j + i] : infty;
                vt[na*j + ka][kb] = i < n ? d_[n*i + j] : infty;
            }
        }
    }
    for (int j = n; j < ncd; ++j) {
        for (int ka = 0; ka < na; ++ka) {
            for (int kb = 0; kb < nb; ++kb) {
                vd[na*j + ka][kb] = infty;
                vt[na*j + ka][kb] = infty;
            }
        }
    }

    #pragma omp parallel for
    for (int ic = 0; ic < nc; ++ic) {
        for (int jc = 0; jc < nc; ++jc) {
            float8_t vv[nd][nd];
            for (int id = 0; id < nd; ++id) {
                for (int jd = 0; jd < nd; ++jd) {
                    vv[id][jd] = f8infty;
                }
            }
            for (int ka = 0; ka < na; ++ka) {
                float8_t y0 = vt[na*(jc * nd + 0) + ka];
                float8_t y1 = vt[na*(jc * nd + 1) + ka];
                float8_t y2 = vt[na*(jc * nd + 2) + ka];
                float8_t x0 = vd[na*(ic * nd + 0) + ka];
                float8_t x1 = vd[na*(ic * nd + 1) + ka];
                float8_t x2 = vd[na*(ic * nd + 2) + ka];
                vv[0][0] = min8(vv[0][0], x0 + y0);
                vv[0][1] = min8(vv[0][1], x0 + y1);
                vv[0][2] = min8(vv[0][2], x0 + y2);
                vv[1][0] = min8(vv[1][0], x1 + y0);
                vv[1][1] = min8(vv[1][1], x1 + y1);
                vv[1][2] = min8(vv[1][2], x1 + y2);
                vv[2][0] = min8(vv[2][0], x2 + y0);
                vv[2][1] = min8(vv[2][1], x2 + y1);
                vv[2][2] = min8(vv[2][2], x2 + y2);
            }
            for (int id = 0; id < nd; ++id) {
                for (int jd = 0; jd < nd; ++jd) {
                    int i = ic * nd + id;
                    int j = jc * nd + jd;
                    if (i < n && j < n) {
                        r[n*i + j] = hmin8(vv[id][jd]);
                    }
                }
            }
        }
    }
}

Results

The code is getting a bit complicated, but it is clearly worth the trouble:

The overall running is now only 1.1 seconds for the multi-threaded version. Recall that our starting point was 99 seconds. By putting together the ideas of multithreading, vector instructions, instruction-level parallelism, and data reuse, we were able to improve the running time by a factor of 91.

We are now using 56% of the theoretical maximum performance of the CPU; we do 35.8 useful arithmetic operations per clock cycle, and the best that we could do with this CPU is 64 additions and/or minimums per clock cycle. If we wanted to improve the running time by more than a factor of two, we would have to invent an entirely new kind of algorithm that solves the problem with less than $n^3$ additions and $n^3$ minimums.

We are very happy now, but of course 56% is still somewhat far from 100%. Could we somehow do better?