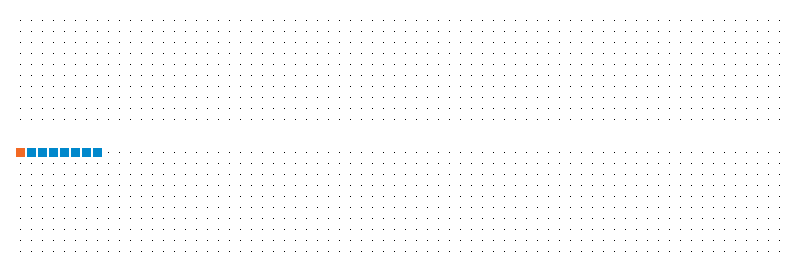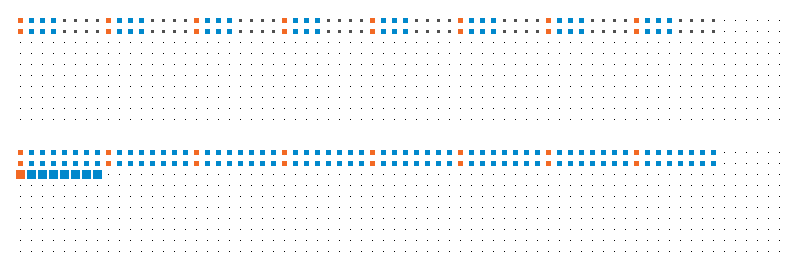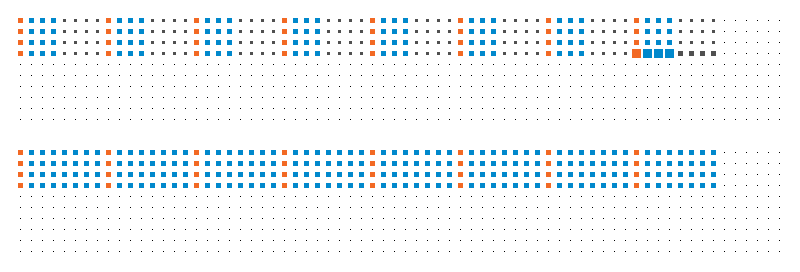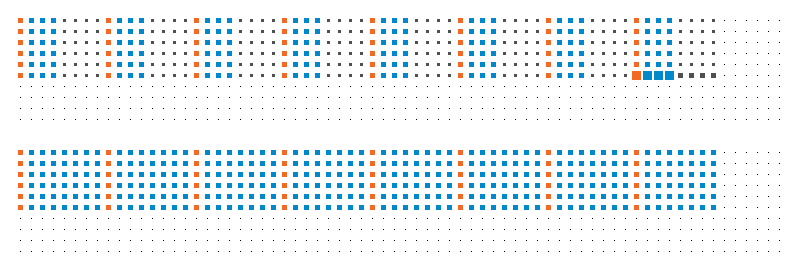Programming Parallel Computers
Version 2: Reuse data in registers
What would be the next steps for improving the performance?
Let us first recall what techniques we used in the CPU version, and what are the analogous concepts in the GPU world. Recall that a warp consists of 32 threads; in our current implementation we have 8 warps per block, and thousands of blocks that are available for execution.
| CPU | GPU |
|---|---|
| Multicore parallelism: multiple threads can be executed simultaneously in parallel. | Multiple warps can be executed simultaneously in parallel. |
| Vector instructions: each vector unit can do 8 similar operations in parallel, one per vector element. | Each warp can do 32 similar operations in parallel, one per thread. |
| Instruction-level parallelism: in each thread we have independent instructions that are ready to be executed while other operations are in the pipeline. | We have got lots of warps that are ready to be executed while other warps are in the pipeline. |
This is good news for us: to fully utilize the arithmetic units of a GPU it is enough to have lots of warps that are ready to be executed, and this is what we are already doing. (This is a bit of an oversimplification, but sufficient for us for now.)
The main bottleneck in our current implementation is not in parallelism but in the memory accesses. In version 0 we had lots of memory accesses, most of them bad from the perspective of the memory system. In version 1 we fixed the memory access pattern so that different threads from the same warp read adjacent memory locations, but we are still doing equally many memory accesses.
To further improve the performance we will need to find a way to do fewer memory accesses. The approach is analogous to what we did with CPUs: heavily reuse data in registers.
Memory access pattern
Our basic idea is similar to Chapter 2, version 5: read 8 + 8 values, do 8 × 8 arithmetic operations, and keep 8 × 8 results in registers. However, this time we do not need to worry about vector registers; we can simply use lots of scalar registers in each thread.
Our main challenge is to find out how to split work between blocks and threads so that we get a nice memory access pattern. We will use the following division of work — it happens to give nice round numbers and it uses a reasonable number of registers:
- Each block consists of 8 × 8 threads.
- Each thread computes 8 × 8 values of the output.
- Each block computes 64 × 64 values of the output.
However, there is a twist: while each block will be responsible for a continuous 64 × 64 region, each thread in the block is calculating discontinuous parts. For example, thread (x, y) in the first block will calculate the following elements of the output:
(0+x, 0+y), (0+x, 8+y), (0+x, 16+y), ..., (0+x, 56+y),
(8+x, 0+y), (8+x, 8+y), (8+x, 16+y), ..., (8+x, 56+y),
...,
(56+x, 0+y), (56+x, 8+y), (56+x, 16+y), ..., (56+x, 56+y),
To see why this would be a good idea, assume that n = 1000 and consider what each thread would be doing. Let d represent the original input matrix and let t be its transpose. Thread (x, y) will read the following elements of the input in this order:
t[0+x], t[8+x], ..., t[56+x],
d[0+y], d[8+y], ..., d[56+y],
t[1000+x], t[1008+x], ..., t[1056+x],
d[1000+y], d[1008+y], ..., d[1056+y],
t[2000+x], t[2008+x], ..., t[2056+x],
d[2000+y], d[2008+y], ..., d[2056+y],
...
At this point the access pattern might not seem to make any sense, but we must always remember to look at it from the perspective of a warp. Recall that a warp consists of 32 threads; for example, the first warp of the first block will consist of threads with the following (x, y) indexes:
(0, 0), (1, 0), (2, 0), ... (7, 0), (0, 1), (1, 1), (2, 1), ... (7, 1), (0, 2), (1, 2), (2, 2), ... (7, 2), (0, 3), (1, 3), (2, 3), ... (7, 3).
Therefore in the first step the threads of the warp would collectively access the following elements:
t[0], t[1], t[2], ..., t[7], t[0], t[1], t[2], ..., t[7], t[0], t[1], t[2], ..., t[7], t[0], t[1], t[2], ..., t[7].
In the second step, the threads of the warp would access the following elements:
t[8], t[9], t[10], ..., t[15], t[8], t[9], t[10], ..., t[15], t[8], t[9], t[10], ..., t[15], t[8], t[9], t[10], ..., t[15].
And later when we start to read from d, the threads of the warp would access these elements:
d[0], d[0], d[0], ...., d[0], d[1], d[1], d[1], ...., d[1], d[2], d[2], d[2], ...., d[2], d[3], d[3], d[3], ...., d[3].
At each point of time, the warp as a whole is accessing some continuous region of memory that fits in a small number of cache lines.
The above animation illustrates what happens in the first block of threads, for the first 6 iterations of the loop:
- Orange: which elements are accessed by the first thread.
- Blue: which elements are accessed by the first warp of threads.
- Black: which elements are accessed by the first block of threads (assuming that they are executing in a synchronized manner, which is not necessarily the case).
- Top: array
d. - Bottom: array
t.
The key observation is that the blue dots always span continuous regions, which is good.
Kernel
Here is the kernel that implements this idea. In preprocessing we will prepare the input array d such that its dimensions are nn × nn, where nn is a multiple of 64. This way we do not need to worry about partial blocks here.
In preprocessing we compute array t, which is the transpose of the input array with a similar padding. We decided to keep d and t in one memory block of dimensions 2 × nn × nn so that we do not need to do that much memory management; hence t starts at address d + nn * nn.
__global__ void mykernel(float* r, const float* d, int n, int nn) {
int ia = threadIdx.x;
int ja = threadIdx.y;
int ic = blockIdx.x;
int jc = blockIdx.y;
const float* t = d + nn * nn;
float v[8][8];
for (int ib = 0; ib < 8; ++ib) {
for (int jb = 0; jb < 8; ++jb) {
v[ib][jb] = HUGE_VALF;
}
}
for (int k = 0; k < n; ++k) {
float x[8];
float y[8];
for (int ib = 0; ib < 8; ++ib) {
int i = ic * 64 + ib * 8 + ia;
x[ib] = t[nn*k + i];
}
for (int jb = 0; jb < 8; ++jb) {
int j = jc * 64 + jb * 8 + ja;
y[jb] = d[nn*k + j];
}
for (int ib = 0; ib < 8; ++ib) {
for (int jb = 0; jb < 8; ++jb) {
v[ib][jb] = min(v[ib][jb], x[ib] + y[jb]);
}
}
}
for (int ib = 0; ib < 8; ++ib) {
for (int jb = 0; jb < 8; ++jb) {
int i = ic * 64 + ib * 8 + ia;
int j = jc * 64 + jb * 8 + ja;
if (i < n && j < n) {
r[n*i + j] = v[ib][jb];
}
}
}
}
Kernel for padding
We define another kernel that takes care of padding and transposing. Again we will need to somehow split this work in blocks and threads. As our input will be padded to a multiple of 64, we decided to organize things as follows:
- One block processes one row of input.
- Each block consists of 64 threads.
- One thread processes 1/64th of a row.
Again we tried to ensure that a warp of threads is doing something meaningful from the perspective of memory accesses. Here, for example, the first warp of the first block will read the following elements in the first iteration of the loop:
r[0], r[1], ..., r[31]
The implementation looks like this:
__global__ void myppkernel(const float* r, float* d, int n, int nn) {
int ja = threadIdx.x;
int i = blockIdx.y;
float* t = d + nn * nn;
for (int jb = 0; jb < nn; jb += 64) {
int j = jb + ja;
float v = (i < n && j < n) ? r[n*i + j] : HUGE_VALF;
d[nn*i + j] = v;
t[nn*j + i] = v;
}
}
CPU side
On the CPU side, the overall idea is this:
- Allocate GPU memory for
rGPUwith dimensions n × n and fordGPUwith dimensions 2 × nn × nn. - Copy
d(input data) torGPU. - Launch
myppkernelthat reads the original input fromrGPUand writes the preprocessed version todGPU. - Launch
mykernelthat reads the preprocessed input fromdGPUand writes the final result torGPU. - Copy
rGPUtor.
Here is the full implementation:
void step(float* r, const float* d, int n) {
int nn = roundup(n, 64);
// Allocate memory & copy data to GPU
float* dGPU = NULL;
CHECK(cudaMalloc((void**)&dGPU, 2 * nn * nn * sizeof(float)));
float* rGPU = NULL;
CHECK(cudaMalloc((void**)&rGPU, n * n * sizeof(float)));
CHECK(cudaMemcpy(rGPU, d, n * n * sizeof(float), cudaMemcpyHostToDevice));
// Run kernel
{
dim3 dimBlock(64, 1);
dim3 dimGrid(1, nn);
myppkernel<<<dimGrid, dimBlock>>>(rGPU, dGPU, n, nn);
CHECK(cudaGetLastError());
}
// Run kernel
{
dim3 dimBlock(8, 8);
dim3 dimGrid(nn / 64, nn / 64);
mykernel<<<dimGrid, dimBlock>>>(rGPU, dGPU, n, nn);
CHECK(cudaGetLastError());
}
// Copy data back to CPU & release memory
CHECK(cudaMemcpy(r, rGPU, n * n * sizeof(float), cudaMemcpyDeviceToHost));
CHECK(cudaFree(dGPU));
CHECK(cudaFree(rGPU));
}
Results
Recall that the previous version took 8 seconds to run. The current version improved the running time to 1.2 seconds; this is already much faster than the fastest CPU solution, which took 2 seconds.
We are now doing 374 operations per clock cycle. This is a very good number: There are 640 arithmetic units in the GPU that can do additions, and only half of them can do also minimums. Even if we had code in which addition and minimum operations were perfectly balanced, we could at best achieve 640 useful operations per clock cycle; hence our performance is already 58 % of the theoretical maximum performance of the GPU. Moreover, our running time includes all overhead related to copying data back and forth between the CPU and the GPU, allocating GPU memory, and launching kernels.